New Approaches To Potential Energy Minimization and Molecular Dynamics
Algorithms
We describe two new algorithms for macromolecular simulations: a truncated
Newton method for potential energy minimization and an implicit integration
scheme for molecular dynamics (MD). The truncated Newton algorithm is specifically
adapted for large-scale potential energy functions. It uses analytic second
derivatives and exploits the separability structure of the Hessian into
bonded and nonbonded terms. The method is rapidly convergent (with a quadratic
convergence rate) and allows variations for avoiding analytic computation
of the nonbonded Hessian terms. The MD algorithm combines the implicit
Euler scheme for integration with the Langevin dynamics formulation.
The implicit scheme permits a wide range of time steps without loss of
numerical stability. In turn, it requires that a nonlinear system be solved
at every step. We accomplish this task by formulating a related minimization
problem-not to be confused with minimization of the potential energy-that
can be solved rapidly with frequency (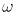 c) which in particular, can be used to mimic the quantum-mechanical discrimination among activity of the various vibrational modes.
c) which in particular, can be used to mimic the quantum-mechanical discrimination among activity of the various vibrational modes.

 Click to go back to the publication list
Click to go back to the publication list
Webpage design by Igor Zilberman

 Click to go back to the publication list
Click to go back to the publication list