Calibration of the Timestep for the Dynamics of Supercoiled DNA modeled
by B-Splines
We address here the correspondence between the physical timestep and the
simulation timestep in our molecular dynamics simulations of supercoiled
DNA modeled by cubic B-splines. The correspondence is not straightforward
since the independent variables in our dynamics are the B-spline control
points rather than the DNA chain points. Since each DNA curve point depends
on four neighboring control points, the effective B-spline mass matrix
is nondiagonal. We derive this matrix rigorously and show that each row
corresponding to a control point has seven nonzero elements. These elements
are configuration dependent and must be computed numerically. We obtain
the rough estimate of 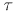 = 100-150
ps for our timestep by equating the expected kinetic energy for the spline
system of DNA - from the classical equipartition theorem - with the computed
kinetic energy using the velocity vectors of the dynamics trajectory and
the spline mass matrix. This estimate lies between our rigorously
calculated lower and upper bounds for
= 100-150
ps for our timestep by equating the expected kinetic energy for the spline
system of DNA - from the classical equipartition theorem - with the computed
kinetic energy using the velocity vectors of the dynamics trajectory and
the spline mass matrix. This estimate lies between our rigorously
calculated lower and upper bounds for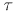 .
A lower bound is obtained by assuming full energy contributions for all
the system's degrees of freedom. An upper bound for
.
A lower bound is obtained by assuming full energy contributions for all
the system's degrees of freedom. An upper bound for 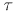 is obtained by estimating the effects of solvent damping and quantum effects,
which together reduce the expected kinetic energy of DNA in its natural
environment. Our resulting timestep estimate corresponds to a difference
of more than three orders of magnitude between our program timestep
is obtained by estimating the effects of solvent damping and quantum effects,
which together reduce the expected kinetic energy of DNA in its natural
environment. Our resulting timestep estimate corresponds to a difference
of more than three orders of magnitude between our program timestep  t
(0.1
ps) and the physical value
t
(0.1
ps) and the physical value 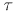 .
.

 Click to go back to the publication list
Click to go back to the publication list
Webpage design by Igor Zilberman

 Click to go back to the publication list
Click to go back to the publication list