Numerical resonance artifacts have become recognized recently as a limiting factor to increasing the timestep in multiple-timestep (MTS) biomolecular dynamics simulations. At certain timesteps correlated to internal motions (e.g., 5 fs, around half the period of the fastest bond stretch, T_min), visible inaccuracies or instabilities can occur. Impulse-MTS schemes are vulnerable to these resonance errors since large energy pulses are introduced to the governing dynamics equations when the slow forces are evaluated. We recently showed that  such resonance artifacts can be masked significantly by applying extrapolative splitting to stochastic dynamics. Theoretical and numerical analyses of force-splitting integrators based on the Verlet discretization are reported here for linear models to explain these observations and suggest how to construct effective integrators for bimolecular dynamics that balance stability with accuracy.

Analyses for Newtonian dynamics demonstrate the severe resonance patterns of the Impulse splitting, with this severity worsening with the outer timestep, t; Constant Extrapolation is  generally unstable, but the disturbances do not grow with t. Thus, the stochastic extrapolative combination can counteract generic instabilities and largely alleviate resonances with a sufficiently strong Langevin heat-bath coupling (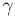), estimates for which are derived here based on the fastest and the slowest motion periods. These resonance results generally hold for nonlinear test systems: a water tetrameter and solvated protein. Proposed related approaches such as Extrapolation/Correction and Midpoint Extrapolation only work better than Constant Extrapolation for timesteps less than T_min/2.

An effective extrapolative stochastic approach for biomolecules that balances long-timestep stability  with good accuracy for the fast subsystem is then applied to a biomolecule using a three-class partitioning: the medium forces are treated by Midpoint Extrapolation via position Verlet, and the slow forces are incorporated by Constant Extrapolation. The resulting algorithm (LN) performs well on a solvated protein system in terms of themodynamical properties and yields an order of magnitude speedup with respect to single-timestep Langevin trajectories. Computed spectral density functions also show how the Newtonian modes can be approximated by using a small 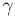 in the range of 5-20 ps^-1.

Click to go back to the publication list

Webpage design by Igor Zilberman