Inherent Speedup Limitations in Multiple Timestep/
Particle Mesh Ewald Algorithms
Multiple timestep (MTS) algorithms present an effective integration approach
to reduce the computational cost of dynamics simulations. By using force
splitting to allow larger timesteps for the more slowly-varying force
components, computational savings can be realized. The Particle-Mesh-Ewald
(PME) method has been independently devised to provide an effective and
efficient treatment of the long-range electrostatics interactions. Here we
examine the performance of a combined MTS/PME algorithm previously developed
for AMBER on a large polymerase 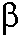 /DNA complex containing 40,673 atoms.
Our goal is to carefully combine the robust features of the Langevin/MTS (LN)
methodology implemented in CHARMM - which uses position rather than velocity
Verlet with stochasticity to make possible outer timesteps of 150 fs - with
the PME formulation. The developed MTS/PME integrator removes fast terms from
the reciprocal-space Ewald component by using switch functions. We analyze the
advantages and limitations of the resulting scheme by comparing performance to
the single timestep leapfrog Verlet integrator currently used in AMBER by
evaluating different timestep protocols using three assessors for accuracy,
speedup, and stability, all applied to long (i.e., nanosecond) simulations to
ensure proper energy conservation. We also examine the performance of the
algorithm on a parallel, distributed shared-memory computer (SGI Origin 2000
with 8 300-MHz R12000 processors). Good energy conservation and stability
behavior can be demonstrated, for Newtonian protocols with outer timesteps of
up to 8 fs and Langevin protocols with outer timesteps of up to 16 fs. Still,
we emphasize in this work the inherent limitations imposed by the
incorporation of MTS methods into the PME formulation that may not be widely
appreciated. Namely, the limiting factor on the largest outer timestep size,
and hence speedup, is an intramolecular cancellation error inherent to PME.
This error stems from the excluded-nonbonded correction term contained in the
reciprocal-space component. This cancellation error varies in time and
introduces artificial frequencies to the governing dynamics motion.
Unfortunately, we find that this numerical PME error cannot be easily
eliminated by refining the PME parameters (grid resolution and/or order of
interpolating polynomial). We suggest that methods other than PME for fast
electrostatics may allow users to reap the full advantages from MTS algorithms.
/DNA complex containing 40,673 atoms.
Our goal is to carefully combine the robust features of the Langevin/MTS (LN)
methodology implemented in CHARMM - which uses position rather than velocity
Verlet with stochasticity to make possible outer timesteps of 150 fs - with
the PME formulation. The developed MTS/PME integrator removes fast terms from
the reciprocal-space Ewald component by using switch functions. We analyze the
advantages and limitations of the resulting scheme by comparing performance to
the single timestep leapfrog Verlet integrator currently used in AMBER by
evaluating different timestep protocols using three assessors for accuracy,
speedup, and stability, all applied to long (i.e., nanosecond) simulations to
ensure proper energy conservation. We also examine the performance of the
algorithm on a parallel, distributed shared-memory computer (SGI Origin 2000
with 8 300-MHz R12000 processors). Good energy conservation and stability
behavior can be demonstrated, for Newtonian protocols with outer timesteps of
up to 8 fs and Langevin protocols with outer timesteps of up to 16 fs. Still,
we emphasize in this work the inherent limitations imposed by the
incorporation of MTS methods into the PME formulation that may not be widely
appreciated. Namely, the limiting factor on the largest outer timestep size,
and hence speedup, is an intramolecular cancellation error inherent to PME.
This error stems from the excluded-nonbonded correction term contained in the
reciprocal-space component. This cancellation error varies in time and
introduces artificial frequencies to the governing dynamics motion.
Unfortunately, we find that this numerical PME error cannot be easily
eliminated by refining the PME parameters (grid resolution and/or order of
interpolating polynomial). We suggest that methods other than PME for fast
electrostatics may allow users to reap the full advantages from MTS algorithms.

 Click to go back to the publication list
Click to go back to the publication list

