Computational Molecular Biophysics Today: A Confluence of Methodical Advances and Complex Biomolecular Applications
1 Introduction
These are exciting times for macromolecular scientists. The efficiency
and resolution of experimental techniques is improving rapidly, bringing
to bear tour-de-force static and dynamic views of large polymeric
systems. Recent examples of such systems include the crystallographically-determined
nucleosome core particle -- an essential building block of the DNA/protein
spools that make up the chromosomal material [1]; unusual conformations
of overstretched DNA and proteins as seen in force-versus-extension
measurements by clever single-molecule manipulations [2] (also reviewed
in [3] for DNA and [4] for the giant muscle molecule titin); competing
unfolding pathways for the small protein barstar -- as obtained by
kinetic studies using spectroscopic probes [5]; folding kinetics of
a catalytic RNA -- as visualized by millisecond time-resolved free
radical cleavage and detected by clever design of mutant fast folders for
which the kinetic trap has been alleviated (reviewed in [6]); and long
buckyball nanotubes -- giant linear fullerene chains that can sustain enormous
elastic deformations [7].
Theoretical modeling is thriving on increased computer power, new algorithmic
ideas from various disciplines, rapid and tantalizing three-dimensional
graphics, and parallel architectural opportunities. Perhaps more than any
other Grand Challenge application today, modeling large biological
polymers -- proteins, nucleic acids, and lipids -- is a truly multidisciplinary
enterprise. In a synergistic fashion, biologists describe the cellular
picture; chemists fill in the atomic and molecular details; physicists
extend these views to the electronic level and the underlying forces; mathematicians
analyze and formulate appropriate numerical models and algorithms; and
computer scientists and engineers provide the crucial implementational
support for running large computer programs on high-speed and extended-communication
platforms.
The immense appeal and interdisciplinary nature of computational molecular
biophysics is largely driven by the many important practical applications
in the field, from drug design to biomedical engineering to food chemistry.
And computational scientists at large are intrigued by the wealth of real
problems that demand sophisticated yet practical algorithms. Such challenging
problems arise, for example, in protein folding prediction, biomolecular
dynamics simulations, genome analysis, and drug design, and involve global
and combinatorial optimization, Hamiltonian and stochastic dynamics, numerical
linear algebra, multivariate statistical analysis, and dynamic programming.
Recognizing the broad theoretical underpinnings and wide application scope
of biomolecular modeling and simulations, the Journal of Computational
Physics welcomes contributions which develop and apply important computational
tools to problems of biological importance. To mark this interest, this
special volume in computational molecular biophysics is dedicated to the
field. Although selective in content and representing only a small number
of research groups, many exciting and active research areas are sampled.
These include various methodologies in molecular dynamics (MD) and quantum-classical
MD simulations (long-time integration schemes, fast electrostatic summation),
configurational sampling and analysis techniques, quantum-mechanical approaches,
and implementation of large simulation programs on high-speed computers.
Various intriguing applications are also included in this volume, involving
thermodynamic and dynamic studies of proteins and various biomolecular
complexes, as found in membrane assemblies, between DNA and proteins, and
between DNA and environmental carcinogens.
2 Algorithmic Advances
The first ten articles of the volume describe various methodological advances.
We open with a general overview and field perspective by Schlick et
al., who focus on algorithmic advances in dynamic simulations (integration,
fast electrostatics) and structure refinement of experimental models. Included
in this review are illustrative macromolecular applications and discussion
of practical implementation of large molecular dynamics programs on parallel
architectures.
2.1 Molecular Dynamics Simulations
MD integration methods are the focus of the four articles. Multiple timestep
(MTS) methods, in particular, are effective techniques for integrating
the classical equations of motion for systems with disparate timescales.
They employ a hierarchical approach for updating the various force components
so that slower forces (e.g., electrostatics) are computed less frequently
than the more rapidly-varying terms (e.g., bonded interactions). This approach
can produce substantial computational savings, since evaluation of the
long-range, slowly-varying terms dominates the force computations. However,
since the force components are intricately coupled, the numerical and physical
behavior of the resulting trajectories depends sensitively on the force
partitioning employed as well as the merging of solution components for
the different force classes. In fact, trajectory-corrupting resonance artifacts
can result at certain protocols (timestep and scheme combinations). Symplectic
methods, for example, have been advocated since they guarantee that for
small timesteps the numerical solution (trajectory) is the exact solution
of a `nearby' Hamiltonian system, a consequence of their strong preservation
of geometric properties of the dynamic flow. However, developing methods
that are accurate and stable over long times and at the same time produce
large computational savings is a current area of active research.
Reich discusses multiple-timestepping schemes for classical MD and extensions
to quantum-classical dynamic models, which treat selected segments of the
molecular system by the time-dependent Schrödinger equation. In this
context, the quantum degrees of freedom are considered fast, and the classical
degrees of freedom are the slow forces. As in classical molecular dynamics
integration, these force components are tightly coupled and cannot be simply
separated. Reich shows that multiple time-stepping schemes can be defined
in a natural way for such quantum-classical MD simulations. Reich also
points to the dangerous consequences of using too large timesteps in such
simulations and concludes that further work is required to design optimal
MTS schemes in this context.
Sandu and Schlick present an extension of MTS schemes to stochastic dynamics
based on the simple Langevin equation. They analyze how a stochastic MTS
treatment can mask resonance artifacts and how best to choose the scheme's
parameters so as to balance accuracy, stability, and computational speed.
An application of the resulting LN method to a solvated protein suggests
that the method can be applied to conformational sampling problems. Further,
the stochastic coupling can be minimized to approximate Newtonian dynamics
as closely as possible. The stochastic formulation of LN yields significant
computational speedup in comparison to symplectic, Newtonian MTS schemes,
and in theory generates the same equilibrium distributions as obtained
from Newtonian trajectories.
Bond, Laird, and Leimkuhler describe a symplectic MD integrator for simulations
performed in the canonical (constant temperature) ensemble. Their method
is based on a Poincaré time transformation of the extended Hamiltonian
model of Nosé. The new method (Nosé-Poincaré) requires
little more computational effort than standard (microcanonical or constant
energy) simulations and samples from the canonical distribution when the
time evolution is ergodic. The Nosé-Poincaré method is applicable
to constrained and rigid-body models, and it can also be used for Nosé-chains.
Lynch, Perkyns, and Pettitt examine the ability of grand canonical ensemble
MD (constant temperature, volume, and chemical potential) based on an extended
Lagrangian approach to predict thermodynamic quantities from microscopic
information. Their study analyzes corresponding number and number fluctuation
averages in the context of the Kirkwood-Buff thermodynamic theory in statistical
mechanics. Results are presented for three water models and suggest that
such Kirkwood-Buff thermodynamic estimates, such as of free energies, can
be obtained readily from constant chemical-potential ensembles and exploited
in the study of biological systems. (See also the article by Jayaram et
al. on free-energy calculations).
2.2 Conformational Analyses
Sampling configuration space efficiently is a major, general challenge
in simulations of biomolecules, at least as important as following fast
processes closely via accurate trajectories of the Hamiltonian. Though
in theory MD simulations can span the large range of thermally accessible
states, computational cost limits the total simulation length that can
be followed. For example, only the nanosecond timeframe is routinely accessible
today for macromolecular systems, a timeframe still very short in comparison
to timescales of large-scale deformations of biological interest. Various
Monte Carlo, hybrid Monte Carlo, and many other sampling procedures have
been developed with this goal, but the key challenge is obtaining good
sampling performance on systems with many degrees of freedom.
Schütte et al. develop a hybrid Monte Carlo procedure for following
essential features of the dynamic evolution of a Hamiltonian system. The
characterization of `essential conformations' and their stability is formulated
in terms of statistical mechanics rather than molecular geometry, specifically
as an almost invariant subset in position space. These conformational
subsets are defined via the discretized eigenvalue problem for a statistically
appropriate spatial transition Markov operator that replaces the Frobenius-Perron
operator (which describes the transition probabilities within a dynamical
system). An appropriate discretization of this operator can make the approach
tractable to molecular systems, as demonstrated for a small RNA system.
Essential conformational features are also examined by Dauber-Osguthorpe
et
al. for a small protein (chymotrypsin-like serine protease) by comparing
signal-processed data from MD trajectories to normal-mode analyses. The
latter technique has been used to characterize a system's motion around
equilibrium on the basis of the same empirical potentials that define the
MD forces. Though normal-mode analysis can describe collective modes of
the system, it is restricted to one region of phase space. In theory, MD
trajectories traverse phase space and offer more information, but good
analytical techniques are needed to extract details from the voluminous
data generated. Through Fourier transforming atomic trajectories and focusing
on frequency ranges of interest, digital processing techniques can reveal
important structural and dynamic information. The current study attempts
to compare results from normal-mode analysis to MD simulations, to compare
theoretical results to experiment, and to characterize the major motion
of the protein that facilitates its binding to a substrate. An overall
qualitatively similar picture of the protein motion is found from both
MD and normal-mode analysis, suggesting a robustness in the protein motion
that is easily captured, specifically a movement of one hairpin loop on
the protein's surface.
Gullingsrud, Braun, and Schulten describe a time series analysis method
for the reconstruction of potentials of mean force from MD trajectories.
Steered Molecular Dynamics (SMD) simulations are used to study protein/ligand
binding and unfolding of proteins at atomic-level detail by mimicking single-molecule
manipulation experiments. Experiment and simulation occur on much different
timescales; hence potential reconstruction is important for relating simulation
results to experimental force versus extension measurements. Three methods
for analyzing time series involving displacement and force data are investigated
and tested on model systems; the most promising method involves minimization
of a Onsager-Machlup functional. Analysis of SMD data for a phospholipid
membrane monolayer system by this method shows the correct reproduction
of the adhesion forces of lipids in membranes, with detailed structural
insights emerging.
2.3 Fast Electrostatics
Boschitsch, Fenley, and Olson describe important algorithmic work in another
area of MD, namely fast evaluation of electrostatic energies and forces
in biomolecular simulations. Various divide-and-conquer approaches have
been developed in the last decade to reduce the direct, 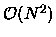 complexity associated with an N-body problem to near linear complexity.
To date, however, most fast multipole methods have focused on purely Coulombic
potentials. These researchers develop a fast multipole expansion based
on spherical modified Bessel functions, which are appropriate for the screened
Coulomb interactions (i.e., Yukawa or Debye-Huckel potentials) used in
modeling polyelectrolytes at various salt concentrations. The performance
of the resulting fast adaptive multipole algorithm (using an octree group
procedure) is evaluated in terms of accuracy and computational time for
various charged systems. Results show the nearly linear scaling complexity
and the robust performance of the method for various charged systems at
different salt concentrations.
complexity associated with an N-body problem to near linear complexity.
To date, however, most fast multipole methods have focused on purely Coulombic
potentials. These researchers develop a fast multipole expansion based
on spherical modified Bessel functions, which are appropriate for the screened
Coulomb interactions (i.e., Yukawa or Debye-Huckel potentials) used in
modeling polyelectrolytes at various salt concentrations. The performance
of the resulting fast adaptive multipole algorithm (using an octree group
procedure) is evaluated in terms of accuracy and computational time for
various charged systems. Results show the nearly linear scaling complexity
and the robust performance of the method for various charged systems at
different salt concentrations.
2.4 Quantum Mechanical Simulations
The electronic description in quantum mechanics is necessary when there
is a change in electronic structure, such as in chemical reactions in enzyme
reactions. Linear scaling quantum mechanical methods are very promising
in meeting the challenge.
Lewis, Liu, Lee, and Yang describe and apply a divide-and-conquer semi-empirical
quantum mechanical technique with linear scaling complexity. The divide-and-conquer
is the first of linear-scaling methods that have made possible quantum
applications to large biological systems. The application to the enzyme
cytidine deaminase examines the reaction pathway of catalysis, involving
a sequence of structural rearrangements that depend on ligand binding.
Structural predictions of the active site under a variety of conditions
are detailed as the enzyme traverses the pathway from ground state to transition
state to product.
3 Design of Molecular Dynamics Programs
Besides new algorithmic developments, efficient implementation of MD programs
for macromolecules is another important area of research. Huber and McCammon
describe an object-oriented library termed OOMPAA in the C++ programming
language for molecular modeling and simulation software. This more modular
and flexible design -- an elaboration of traditional subroutine-oriented
code structure -- facilitates code modification and expansion. Their performance
evaluation on pairwise summation computations indicates competitiveness
with respect to traditional Fortran codes.
The Illinois program NAMD2 described by Kalé et al. is specifically
tailored to parallel computing platforms. Through a multidisciplinary collaboration,
its features are continuously adapted to the application needs of biophysicists.
NAMD2 is also implemented using a modular C++ design, and uses data-driven
objects, and object-migration based load balancing supported in Charm++,
a parallel C++ library. NAMD2 uses spatial decomposition combined with
force decomposition to enhance scalability on various parallel architectures.
The performance efficiency of NAMD2 on 220 processors (namely parallel
speedup of 180, or around 80% efficiency) is impressive and might further
be improved through communication-overhead reduction.
4 Biomolecular Applications
To make biomolecular simulation studies physically relevant, modeling ingenuity
and algorithmic tailoring is often required to treat large complex systems.
The five biomolecular applications presented next in the volume require
such tailoring: efficient configurational sampling guided by experimental
data, efficient global optimization procedures for protein folding, free-energy
simulation protocols for molecular complexes, simulation protocols for
supramolecular systems, and homology-based protocols for protein structure
prediction.
4.1 Biomolecular Interactions and Complexes
Broyde and Hingerty describe the development of effective conformational
search techniques for identifying novel geometries of DNA bound covalently
to environmental aromatic carcinogens (carcinogen-DNA adducts). Understanding
energetic and dynamic features of such systems is important for correlating
adduct type with mutagenic and tumorigenic tendencies on the basis of structural
deformations at the DNA level. The search techniques summarized in this
review involve wide-scale conformational searches with systematic buildup,
and minimization in torsion-angle rather than Cartesian space, thereby
reducing markedly the number of free conformational variables. Penalty
functions are applied optionally to selected distances to locate structures
within the bounds of experimentally-derived NMR interproton values and
to search for selected DNA hydrogen bonding patterns. Predictions employing
these approaches are in agreement with high-resolution NMR studies in solution.
Moreover, the geometric features discerned for distinct classes of carcinogen-bound
DNAs have suggested how to relate structural effects with the complex biological
pathways involved in mutagenesis and tumorigenesis. In particular, the
predicted and observed phenomenon of opposite orientation along the DNA
in adducts stemming from chiral chemical reactants with different tumorigenic
potencies has established a structure/function theme that applies more
generally.
Characterizing binding interactions among biomolecular systems is another
important goal in computational molecular biophysics. Jayaram et al.
detail a thermodynamic and functional analysis of a protein/DNA complex
(restriction enzyme EcoRI endonuclease bound to its cognate DNA in solution)
using free-energy simulation methodology with a careful electrostatic treatment.
Free-energy simulations attempt to follow a conformational change or reaction
by defining a specific reaction coordinate and are generally subject to
large errors and protocol sensitivity. With care, however, as done in this
work, insights into the molecular process which cannot be obtained by other
techniques can emerge. These researchers analyzed the calculated free energy
of binding in terms of various energetic contributions (electrostatics,
van der Waals, hydrophobic effects) and their influence on the binding
process (favoring or disfavoring complexation) at the residue level (nucleotide
and amino acid). The energy of solvation in particular is found to be important,
with van der Waals interactions and water release favoring binding, and
electrostatic interactions (intramolecular and solvation) proving unfavorable
to the reaction.
Duong, Mehler and Weinstein propose an appropriate MD protocol for a complex
membrane bilayer system by considering various electrostatic treatments
and trajectory ensembles (microcanonical vs. isothermal-isobaric, i.e.,
constant energy and volume vs. constant temperature and pressure). The
nanosecond-range simulations reveal detailed structural and dynamic characteristics
of the system's components (lipid hydrocarbon chains, polar head groups,
water) that compare favorably with experimental data. Of the simulation
protocols tested, the microcanonical ensemble/truncated electrostatics
combination, with sufficient equilibration, yielded a membrane structure
with properties in best agreement with experiment. The dynamic behavior
of a membrane/peptide complex is then explored to probe atomic details
of the segment's stabilization by the membrane. The modeled peptide is
one transmembrane segment of a G protein coupled receptor that is important
for signal transduction processes. The model incorporates a proline-kink
that perturbs the 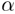 -helical
structure, exposing polar groups to the membrane environment. Analysis
of the flexibility of the bend angle at the junction between the two
-helical
structure, exposing polar groups to the membrane environment. Analysis
of the flexibility of the bend angle at the junction between the two 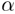 -helical
domains flanking the proline in the transmembrane segment and of the hydrogen-bonding
organization reveals the strong topological and energetic boundary forces
produced by the lipid bilayer. It also demonstrates the importance of the
membrane-penetrating water molecules in stabilizing the polar segments
of the perturbed
-helical
domains flanking the proline in the transmembrane segment and of the hydrogen-bonding
organization reveals the strong topological and energetic boundary forces
produced by the lipid bilayer. It also demonstrates the importance of the
membrane-penetrating water molecules in stabilizing the polar segments
of the perturbed 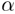 -helical
peptide in the membrane environment.
-helical
peptide in the membrane environment.
4.2 In Silico Protein Folding
Protein structure prediction is a well known goal in molecular biophysics,
with research advances even making headlines in The New York Times
and The Wall Street Journal. Sánchez and Sali review the
state-of-the-art in homology-based structure prediction. Such comparative
modeling works -- structure prediction based on sequence similarity --
are becoming increasingly valuable with the rapidly growing information
on genomic sequences. This class of methods appears to be the only one
at present among theoretical prediction techniques that can yield sufficient
accuracy of protein models (e.g., 2 Å resolution) to be useful for
biological applications (e.g., ligand design, protein engineering). In
general, a large sequence homology (e.g., > 40%) usually implies great
structure similarity (as characterized by a similar overall fold).
The authors describe available methods for homology-based protein structure
prediction, discuss prospects for their automation, and advocate that a
focused, large-scale structural genomics effort (experimental and theoretical)
is needed to reliably determine three-dimensional (3D) protein structures
from the wealth of rising sequence information. In particular, they advocate
that target sequences for structure determination by both experimentalists
and theorists should be selected based on their potential to produce new
structural motifs (folds), so that eventually these cataloged patterns
-- the number of which is thought be be finite -- could be nearly exhausted.
Abagyan and Totrov describe alternative prediction methods for polypeptide
and protein 3D structure termed ab initio. Such methods essentially
attempt to predict 3D structures from sequence alone; they employ an empirical
objective function representing interaction energies (and sometimes statistical
information) in combination with selected sampling strategies. The energy
function used by Abagyan and Totrov is based on an all-atom vacuo potential
developed by Scheraga and co-workers (ECEPP) with added terms to account
for the solvation free energy (on the basis of solvent accessible surfaces)
and entropy (based on residue burial entropies). For efficient sampling
of conformation space, the researchers advocate stochastic global optimization
techniques, involving full local minimization after each random move. Specifically,
they describe an ``Optimal-bias Monte Carlo minimization'' algorithm in
dihedral-variable (rather than Cartesian) space that employs biased moves
predetermined according to local probability distributions of the conformational
variables. The method is shown to perform efficiently on several peptides
and to find the global minimum for a 23-residue peptide.
5 On The Horizon
The methodological and application studies collected in this volume reflect
only a tip of giant iceberg that continuously grows. With the exponential
increase in genomic information, multidisciplinary collaborations are needed
more than ever to tackle the technological and scientific challenges that
are emerging in our era of overwhelming biological information. Solving
these many challenges in macromolecular structure will constitute a giant
leap in our ability to design new pharmaceuticals and materials, and to
exploit functional properties of new gene products for virtually every
aspect of our lives. One can readily envision as a result the development
of designer foods that fight diseases, engineering of improved computer
chips or new architectural components (e.g., for bridges) that can sustain
enormous structural deformations, and powerful vaccines to stave off human
foes.
Will we eventually succeed in reliably predicting 3D structures of proteins
from sequence? If so, will this `Holy Grail' be solved by an accurate physical
description of the underlying forces, a wealth of experimental information,
or some combination? Will methodological advances eventually conquer the
sampling problem, both in space (global optimization) and time (as in molecular
dynamics) for large-scale chaotic systems?
In only twenty years the field has evolved impressively from simulations
of simplified biomolecular systems represented by only a few dozen atoms
covering a fraction of a picosecond to those following intricate biomolecular
complexes approaching one million atoms over timescales that are 4 and
5 orders of magnitude longer. Yet the underlying empirical nature of the
governing energy function cannot be ignored; even the fastest computers
and the most exhaustive conformational searches may not lead to perfect
answers to make the experimentalist's workbench obsolete. Yet perfection
is not a realistic goal for computational biomolecular scientists. Rather,
good approximations to complex real problems can be far more insightful
in this field than exact solutions to ideal questions. Thus, at this crucial
juncture between the rapidly improving theoretical and experimental techniques,
reserved optimism is prudent. I hesitate to predict what a journal volume
of this nature will contain a decade from now, but I certainly look forward
to the discoveries.
Tamar Schlick
Bibliography
1 K. Luger, A. W. Mäder, R. K. Richmond, D. F. Sargent, and T. J.
Richmond.
Crystal structure of the nucleosome core particle
at 2.8 Å resolution.
Nature, 389:251-260, 1997.
2 Frontiers in chemistry: Single molecules. Special section of articles
in
Science, 283:1667-1695, 1999.
3 A. Rich.
The rise of single-molecule DNA chemistry.
Proc. Natl. Acad. Sci. USA, 95:13999-14000,
1998.
4 W. A. Linke and H. Granzier.
A spring tale: New facts on titin elasticity.
Biophys. J., 75:2613-2615, 1998.
5 F. N. Zaidi, U. Nath, and J. B. Udgaonkar.
Multiple intermediates and transition states
during protein unfolding.
Nature Struc. Biol., 4:1016-1024, 1997.
6 R. T. Batey and J. A. Doudna.
The parallel universe of RNA folding.
Nature Struc. Biol., 5:337-340, 1998.
7 B. I. Yakobson and R. E. Smalley.
Fullerene nanotubes: C 1,000,000 and beyond.
Amer. Sci., 85:324-337, 1997.
Postcript and
PDF versions of the full length paper are available.

 Click
to go back to the publication list
Click
to go back to the publication list
Webpage design by Igor Zilberman

 Click
to go back to the publication list
Click
to go back to the publication list