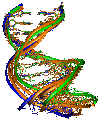RNA graph theory and RNA-As-Graphs (RAG) web resource
The Schlick lab has developed a theoretical framework for RNA analysis and design based on graph theory and computational methods (Gan et al., 2003). Graph theory is a field in mathematics widely used for analyzing networks and enumerating structural possibilities, including chemical structures (e.g., hydrocarbons, drug compounds, and polymer networks), genetic and biochemical networks, transportation, and the Internet. It has already been used for analysis of RNA secondary structures in pioneering works by M. Waterman, B. A. Shapiro, and others. In addition to the familiar tree graphs, we have developed RNA dual graphs (see Figure 4) and demonstrated the potential of graph theory as a mathematical tool for enumerating and constructing all possible RNA tree and pseudoknot motifs, some of which may be either naturally occurring or generated in the laboratory. Significantly, the graph theory approach predicts many new RNA-like motifs (see Figure 5); these can be used to guide the search for novel RNAs in genomes and experimental in vitro selection of functional RNAs2. We have used RNA graphs to: (a) classify and catalog all RNA motifs (Fera et al., 2004; Gan et al., 2004; Kim et al., 2004); (b) estimate the size of RNA's structural/functional repertoire (Kim et al., 2004); (c) design structurally diverse RNA pools to enhance in vitro selection of functional RNAs (Kim et al., 2007a; Kim et al., 2007c); and (d) detect structural and functional similarity among existing RNAs (Pasquali et al., 2005).
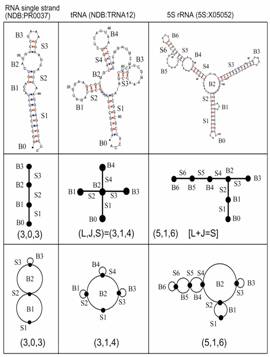
Figure 4. Graphical representations of RNA secondary structures (top) as tree (middle) and dual (bottom) graphs.
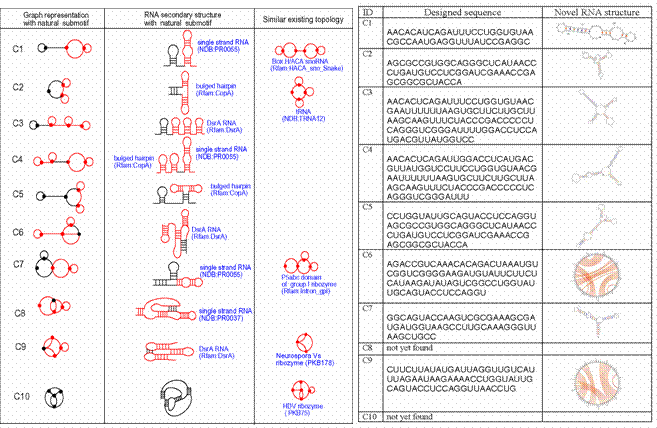
Figure 5. (Left) Ten examples of predicted novel RNA-like (dual graph) topologies (1st column, labeled C1,…,C10) shown with their secondary structures (2nd column) and natural submotifs (red lines). (Right) Designed sequences that fold to RNA-like motifs using a modular assembly approach where fragments from existing RNAs are assembled and folded. C6 and C9 are pseudoknot folds.
By using the RNA graph-based techniques, our lab has established an RNA-As-Graphs (RAG) web resource which archives natural, “missing” RNA-like, and hypothetical motifs; see RAG for tutorials on RNA graph representations. To discover the missing motifs, we are collaborating with experimentalists to identify novel synthetic RNAs via in vitro selection. See Modeling of in vitro selection of RNAs and our RAGPOOLS web server for details on RNA in vitro selection and design of RNA pools using graphs.


Fig. 6. RNA web resource and server based on RNA graphs developed by the Schlick group. RAG catalogues existing, probable and hypothetical RNA motifs. RAGPOOLS enables analysis and design of RNA pools using RNA graphs.
RNA tertiary motifs
RNA tertiary motifs play an important role in RNA folding and biochemical functions. To help interpret the complex organization of RNA tertiary interactions, we comprehensively analyze a dataset of 54 high-resolution RNA crystal structures for motif occurrence and correlations (Xin, Laing et al. 2008). Specifically, we search seven recognized categories of RNA tertiary motifs (coaxial helix, A-minor, ribose zipper, pseudoknot, kissing hairpin, tRNA D-loop/T-loop and tetraloop-tetraloop receptor) by various computer programs. For the non-redundant RNA dataset, we find 615 RNA tertiary interactions (Fig. 7a), most of which occur in the 16S and 23S rRNAs. An exhaustive analysis of these motifs reveals the diversity and variety of A-minor motif interactions and various possible loop-loop receptor interactions that expand upon the tetraloop-tetraloop receptor. Correlations between motifs, such as pseudoknot or coaxial helix with A-minor, reveal higher-order patterns (Fig. 7b). These findings may help define tertiary structure restraints for RNA tertiary structure prediction. A complete annotation of the RNA diagrams for our dataset is available at http://www.biomath.nyu.edu/biomath/motifs/index.html
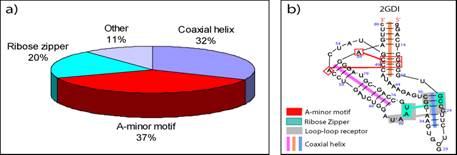
Figure 7 (a) The distribution of RNA tertiary motifs in the non-redundant dataset of 54 high-resolution crystal structures. (b) Annotated diagram of the TPP riboswitch (PDB: 2GDI) shows several correlated motifs.
RNA secondary structures can be divided into helical regions composed of canonical Watson-Crick and related basepairs, as well as single-stranded regions such as hairpin loops, internal loops, and junctions. These elements function as building blocks in the design of diverse RNA molecules with various fundamental functions in the cell. To better understand the intricate architecture of three-dimensional RNAs, we analyze existing RNA junctions in terms of basepair interactions and three-dimensional configurations (Laing and Schlick, 2009; Laing et al., 2009). First, we study base pair interaction diagrams for solved RNA junctions and examine common features. Second, we compare junctions with five to ten helices to those containing three or four helices and identify global motif patterns. In agreement with previous studies, we suggest that coaxial stacking between helices likely forms when the common single stranded loop is small in size; however, other factors such as stacking interactions involving non-canonical base pairs and proteins can greatly determine or disrupt coaxial stacking. We identified nine major four-way (four helices) junction families according to coaxial stacking patterns and helical configurations (see Fig. 8a). The study indicates that helices within junctions tend to arrange in roughly parallel and perpendicular patterns, and stabilize their conformations using common tertiary motifs like coaxial stacking, loop-helix interaction, and helix packing interaction (see Fig. 8b).
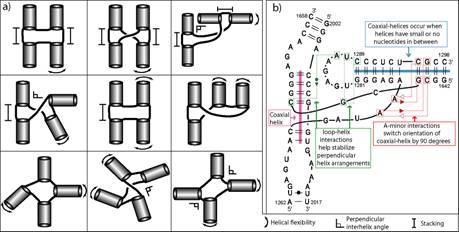
Fig. 8 a) Classification of RNA four-way junctions into nine families according to their coaxial stacking properties and flexible helical arms. b) Diagram of a four-way junction composed of two coaxial helices arranged in a perpendicular fashion. The conformation is stabilized by key 3D motifs.
The study also underscores the notion that RNA junctions are composed of both rigid and flexible elements. Tertiary motifs such as coaxial stacking are interactions responsible for maintaining the rigid parts of the junction, while flexible elements appear on helical arms with longer loop regions and are more sensitive to external forces such as proteins and ion concentration.
We also have introduced the ribo-base interactions: when combined with the along-groove packing motif, these ribo-base interactions form novel motifs involved in perpendicular helix-helix interactions (see Fig. 9a). In addition, these analyses show that higher order junctions organize their helical components as sub-junctions that resemble local helical configurations found in three and four-way junctions (see Fig. 9b).
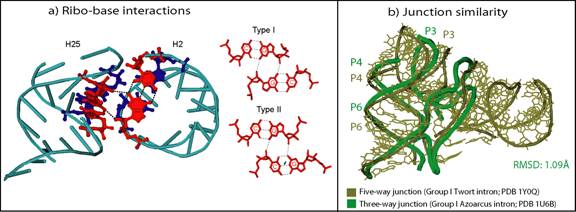
Figure 9 (a) Perpendicular interaction of helices H2 and H25 in the 23S rRNA (PDB 2J01) formed by one of the two types of ribo-base interactions we have identified (b) Structural similarity between a three-way junction and a five-way junction shows Nature’s preference for similar helical organization in all junctions.
Overall, these analyses suggest recurrent tertiary motifs that stabilize junction architecture, pack helices, and help form helical configurations that occur as sub-elements of larger junction networks. The frequent occurrence of similar helical motifs suggest Nature’s finite and perhaps limited repertoire of RNA helical conformation preferences. More generally, studies of RNA junctions and tertiary building blocks can ultimately help in the difficult task of RNA 3D structure prediction.
Modeling of in vitro selection of RNAs
In vitro selection is an experimental method for screening large random-sequence libraries of nucleic acid molecules (~1015) for a specific function, such as binding or catalysis (Ellington and Szostak, 1990; Jaschke, 2001; Storz, 2002; Tuerk and Gold, 1990; Wilson and Szostak, 1999). The versatility of the method has led to numerous nucleic acid molecules binding targets (aptamers) as diverse as organic molecules, antibiotics, proteins, and whole viruses (Hermann and Patel, 2000; Wilson and Szostak, 1999). Importantly, in vitro selection experiments have enabled discovery of new classes of RNA enzymes (ribozymes) and have ramifications for biomolecular engineering, e.g., design of allosteric ribozymes and aptamer-based biosensors (Soukup and Breaker, 1999a; Soukup and Breaker, 1999b; Soukup and Breaker, 2000), and aptamers capable of inhibiting protein function for functional genomics; (Famulok and Verma, 2002; Toulme et al., 2004) many aptamers and ribozymes have also been developed for therapeutic applications (Peracchi, 2004; Bagheri and Kashani-Sabet, 2004).
Current in vitro selection approaches, however, have inherent limitations, including non-exhaustive coverage of sequence space and prevalence of simple topological motifs (e.g., stem-loop, stem-bulge-stem-loop). To improve RNA in vitro selection technology, synthesized RNA pools must possess sufficient sequence and structural complexity to enable discovery of complex RNA molecules (e.g., allosteric ribozymes).
Our research aims to model the processes of in vitro selection, including pool synthesis and motif selection to link theory with experiment, and analyze, design, and test RNA pools to enhance in vitro selection experiments. Recently, we have made progress in analysis and design of sequence pools. We showed quantitatively after simulating in vitro RNA pools that random pools are not structurally diverse, confirming results from various in vitro selection experiments (Gevertz et al., 2005). We have also developed an automated algorithm for designing pools with user-specified target structural distribution (e.g., specific topological structures or graphs representing RNA trees) (Kim et al., 2007a; Kim et al., 2007b). The algorithm optimizes the nucleotide mixing matrix or nucleotide mixing ratios in synthesis ports. It is implemented in a web server we call RAGPOOLS (http://rubin2.biomath.nyu.edu ) to allow experimentalists and other researchers to analyze and design RNA pools (Kim et al., 2007b).
Essentially, our pool engineering incorporates the complexity of secondary structure space as described by our RNA graph theory (Gan et al., 2003; Gan et al., 2004; Kim et al., 2004). Designed pools with a good coverage of the secondary structure space are more likely to yield functional RNAs than random sequence pools since an RNA’s functional properties strongly correlate with corresponding secondary rather than primary structure. To meet this challenge, our RNA pool design strategies incorporate elements of graph theory analysis of pool structures and biased pool synthesis via the mixing matrix, as well as application of applied mathematics techniques to analyze sequence/structure space to ensure structural diversity in designed pools. Figure 10 illustrates our theoretical modeling of RNA in vitro selection.
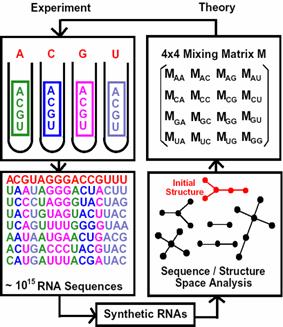
Figure 10. Scheme of experimental RNA pool synthesis, and in vitro selection (left), and theoretical modeling of pool generation using the mixing matrix, which specifies nucleotide mixtures in synthesis ports or mutation rates for all nucleotide bases (right). Our design methods target specific pool sequence and structural properties to produce different mixing matrices that can be exploited by in vitro selection of RNAs.
For a full description of pool design with mixing matrices, visit our RAGPOOLS server which contains tutorials on mixing matrices, analysis of RNA motif distribution, and algorithms for structured pool design, as well as examples of designed pools.
Another topic of interest to us is theoretical modeling of in vitro/directed evolution, an experimental method for refining RNA function via cycles of mutations and function selection (Joyce, 2004). Theoretical modeling of RNA in vitro selection and direct evolution requires close collaborations with experimentalists, a deep understanding of the relation between RNA structure and function, and innovative computational techniques to model aspects of the experimental technology (i.e., pool synthesis, RNA selection and evolution).
Complementary approaches to RNA structure and function
Estimating the fraction of noncoding RNAs in mammalian transcriptomes. Recent studies of mammalian transcriptomes (total expressed RNA transcripts in cells) have identified numerous RNA transcripts that do not code for proteins; their identity, however, is largely unknown. Attempting to determine whether these putative ncRNAs are functional, we developed an approximation model to assess the fraction of genuine ncRNAs in putative ncRNA datasets. We used George Marsaglia’s randomness test from the theory of random number generators (RNG) to derive a measure (the relative z-score) that characterizes global features of RNA sequence classes (Xin et al., 2008); see Figure 11. Significantly, it leads to a fractional ncRNA measure of putative ncRNA datasets which we modeled as a mixture of genuine ncRNAs and other transcripts derived from genomic, intergenic and intronic sequences. We used this model to analyze ncRNA datasets from the FANTOM3 project and two computational approaches based on comparative analysis (RNAz and EvoFold). Our analysis suggests a wide range of ncRNA fractions (5–50%) in these datasets, implying that current putative ncRNA datasets from cDNA sequencing and comparative analysis may overestimate the number of genuine ncRNAs.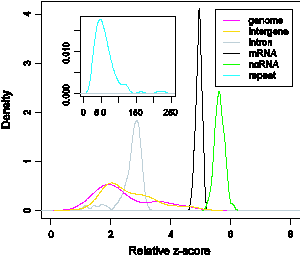
Figure 11. Degree of randomness (relative z-score) distribution of various nucleotide sequence classes. The mRNA (black) and ncRNA (green) classes are less random than the intron class (gray).
Antibotics targeting the ribosome. We are combining computational and experimental approaches to identify novel target sites for antibiotics on bacterial ribosomal RNAs. The computational work involves assessing the energetics of antibiotic/rRNA binding and relating sequence conservation to phenotypes of rRNA mutations. This work is being pursued in collaboration with the laboratory of Ada Yonath (Weizmann Institute, Israel).