How to Represent All Types of RNA Motifs as Dual Graphs
RNA tree graphs convey the connectivity of secondary elements. These secondary elements include junctions, internal loops, hairpin loops, bulges, and stems.

The following explains how dual graph edges and vertices are assigned:
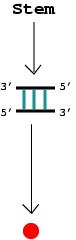
1. An RNA stem that posesses more than one complementary base pair is represented by a vertex.
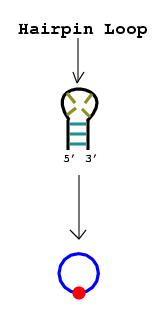
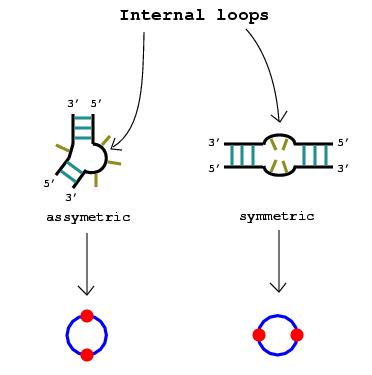
2. Nucleotide bulges, hairpin loops, or internal loops with more than one non-complementary base pair or more than three unmatched nucleotides are represented by circular edges. The RNA stems that surround these bulges and loops are drawn as vertices lying upon the circular edges.
Note: If only one base pair separates what would otherwise be considered a bulge or a loop, that pair can be disregarded since a stem technically consists of at least two consecutive complementary base pairs.
|
|
|
 |
3. A junction is also drawn as a circle.
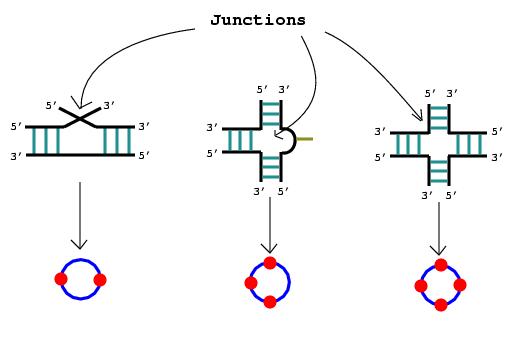
4. No representation is required for the 3' and 5' ends of an RNA molecule.
We emphasize that these simplified dual graphs only model topological, rather than geometric, aspects of RNA molecules; for example, they do not tell us the relative angles between stems. By matching the graphs to real RNAs, we can infer the average length of stems, the average size of junctions and the average number of nucleotides in loops and bulges. For example, an edge represents a stem of about 20 nt. Thus a four-edge graph for tRNA corresponds roughly to an 80 nt. RNA.
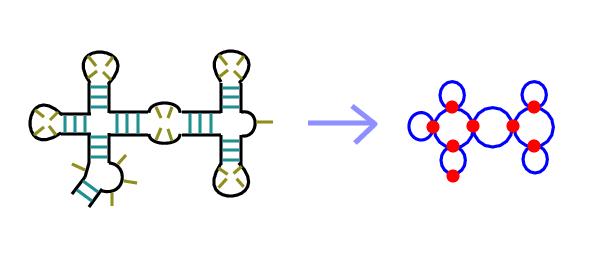
The following example shows how these rules are applied to generate a dual graph:
Properties of RNA dual graphs
RNA secondary structures represented as dual graphs have specific connectivity properties. A double-stranded RNA stem is connected to at most 2 strands on either ends for a total of 4 strands. This means that the maximum number of incident edges at any vertex (i.e., edges emanating from a vertex) of a dual graph is 4, except for one or two vertices which may have 2 or 3 incident edges.
The vertices with two/three incident edges indicate where one/both ends (3' and 5') is/are located. If two vertices have less than 4 incident edges, both must have 3 incident edges. On the other hand, if all vertices have 4 incident edges except one, that vertex must have two incident edges. These properties imply a total of 2V-1 edges for any V-vertex RNA dual graph.